El cálculo de precio de una opción es complejo. Pero por lo general, la prima (precio) de una opción se divide en 2 partes:
- Prima intrínseca (que no siempre la tiene). Realmente es el valor actual que tiene la opción si hoy mismo venciera. Es, por decirlo de otra forma, la cantidad que la opción está dentro del dinero. Si no está dentro del dinero no tiene valor intrínseco.
- Prima extrínseca (que siempre tiene). Es el valor del precio que corresponde al tiempo restante de vida que tiene la opción. Y esto depende de los días que quedan hasta su vencimiento y los actuales niveles de movimiento en el mercado actual (la volatilidad).
Las griegas que influyen en la prima intrínseca son Delta y Gamma. Y las griegas que más tienen que ver con la prima extrínseca son Theta y Vega.
Las griegas Influyen de una forma directa sobre el precio de la opción y son vitales para gestionar nuestras posiciones.
En este artículo vamos a analizar la griega Vega.
Vega
La vega es el cambio en el precio de la opción por una variación en la volatilidad de un 1%. Primero vamos a analizar lo que es la volatilidad.
Volatilidad significa movimiento. La definición exacta es ‘Una medida de la frecuencia e intensidad de los cambios del precio de un activo o de un tipo’. Cuanto más movimiento tiene un valor más volátil es. Una volatilidad alta quiere decir que el precio de un valor o subyacente puede cambiar mucho tanto arriba como abajo en cortos periodos de tiempo. Una volatilidad baja significa que el precio del valor o subyacente no fluctúa mucho, pero cambia de una forma estable durante un periodo de tiempo.
Existen muchas fórmulas complejas para calcular la volatilidad, pero no es imprescindible que las sepamos. Es más, hoy en día la mayoría de las plataformas y software de opciones calculan varios tipos de volatilidades. Un método rápido para calcular hasta qué punto un subyacente se está moviendo mucho o poco es a través de su desviación estándar (standard deviation). O bien para un día, para 20 días o para un año. Una desviación estándar es el término estadístico que mide la desviación de un subyacente respecto a su valor medio. El rango dentro del cual el subyacente ha estado moviéndose en un 68% de las veces es una desviación estándar. Así que una desviación estándar es un 68%, dos desviaciones estándares son un 95% y tres un 99%. Aproximadamente dos tercios de los movimientos del subyacente en un determinado periodo ocurren dentro de una desviación estándar, arriba o abajo.
Por ejemplo, si XYZ tiene una volatilidad anual de un 30% y su precio está a 500, se moverá entre 650 (30% arriba) y 350 (30% abajo) un 68% del tiempo. Este tipo de volatilidad es histórica, basada en los movimientos del subyacente del pasado.
Volatilidad implícita es la volatilidad futura que el mercado prevé para la opción. Todos los otros componentes para calcular el precio de una opción son constantes: precio de subyacente, precio de strike, tipos de interés, dividendos y tiempo hasta vencimiento. Ellos componen lo que es la parte teórica del precio. Sin embargo, a veces hay más o menos demanda para ciertas opciones y como consecuencia el precio varía. La parte que varía es lo que corresponde a la volatilidad implícita. Cuando hay más demanda y se paga más por una opción, el incremento en la prima se achaca a la volatilidad implícita y esta sube. Pasa mucho por ejemplo cuando el mercado baja, los inversores buscan comprar puts para proteger sus posiciones largas de acciones y tanto los precios como ‘el miedo’ (la volatilidad) incrementa y todo encarece. Suele haber menos demanda por opciones cuando hay más tranquilidad en el mercado. Esto junto con el hecho de que hay menos ‘miedo’ (volatilidad) en el mercado abarata las opciones. La volatilidad implícita es un reflejo de la demanda que existe para las opciones.
Una cuestión planteada frecuentemente por los traders es si la volatilidad implícita está alta o baja en comparación a la histórica. Por ejemplo, estando los niveles actuales de la implícita por debajo de los de la histórica nos preguntaríamos si merece la pena, o no, ¿comprar volatilidad implícita pensando en que subirá a niveles de la histórica?

En el gráfico vemos la volatilidad implícita (azul) y volatilidad histórica (‘statistical’, púrpura) de un año para GOOG. Muestra como hay un constante cambio de una volatilidad estando por encima o por abajo de la otra.
Cuando compramos opciones, compramos vega, estamos vega positiva, largos de vega. Cuando vendemos opciones, vendemos vega, estamos vega negativa, cortos de vega.
Si estamos largos de vega y la volatilidad implícita sube nuestra posición incrementa en valor. Si la volatilidad implícita baja perjudica nuestra posición. Si estamos cortos de vega es al revés, una subida en la volatilidad implícita perjudica nuestra posición y la beneficia si baja.
Es muy importante entender que por mucho que suba y baje la volatilidad durante la vida de una opción, al final del trayecto se quedará en nada. La volatilidad forma parte del valor extrínseco de una opción, igual que la theta, y que el día de vencimiento, lo único que cuenta es el valor intrínseco, la cantidad que la opción está dentro del dinero. Todo lo demás, tanto theta como vega, habrá acabado, sin más más posibilidades, esperanzas, promesas, rumores etc de nada. A fin de cuenta esto es lo que significa el valor extrínseco, la prima de tiempo.
Tal como la gamma y la theta, la vega está en su punto más alto (más sensible) en las opciones ATM. Sin embargo, a diferencia que la gamma y la vega, cuanto más lejano esté el mes de vencimiento mayor es la vega. Esto es porque como hay más tiempo de vida de la opción mayor incertidumbre hay sobre si terminará en el dinero o no.
Tabla de la Sensibilidad de Vega en una Cadena de Opciones
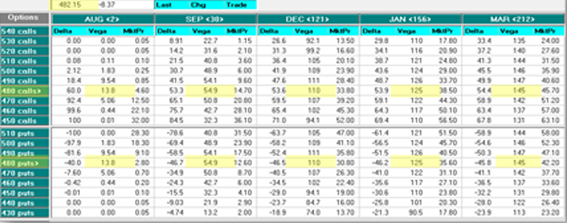
En la tabla de opciones de arriba vemos como la vega en las opciones ATM es la más alta. Y la vega crece conforme vayamos alejándonos en tiempo. Por ejemplo, para la call 480 la vega sube de 54,9 en el mes de septiembre a 110 en el mes de diciembre. Esto quiere decir que para la 480 call cada incremento de un 1% en su volatilidad implícita sube la prima de la opción en $110, siempre y cuando todos los otros variables se mantengan iguales.
Ahora vemos gráficamente como la vega y la volatilidad pueden beneficiarnos y perjudicarnos. Estamos largos de volatilidad con un Aug 500 cono comprado. La vega de la call 500 como la put 500 es de 40. Estamos largos en 80 vega. La volatilidad implícita de las dos opciones es de un 30%. Vemos que gráficamente a través de la línea T+0 (el presente día) el efecto que tiene cambios en la volatilidad sobre nuestra posición es parecido al efecto que tiene la theta, todo el gráfico (toda la posición) sube arriba o abajo.
Cambios de VI en un Cono Comprado
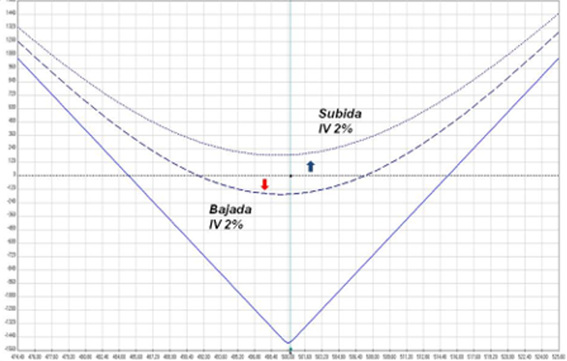
En este caso, si la volatilidad implícita (VI) de las opciones sube en 2 puntos porcentuales a un 32% (y todos los otros variables quedan iguales) nuestra posición incrementará $160 en valor (40 x 2 x 2 = 160). La línea de puntitos (T+0) está claramente en beneficios. Si la VI de las opciones baja en 2 puntos porcentuales a un 28%, nos perjudicará en la misma cantidad, $160. La línea intermitente (T+0) está claramente en pérdidas.
Y si estamos vendidos del cono, es igual, pero al revés. Ahora hemos vendido vega. Estamos cortos 80 vega. Si la VI sube 2 puntos a 32%, nos perjudica ya que cuando la vendimos valía menos que ahora. Estaríamos perdiendo $160 (con todos los otros variables iguales).
Cambios de VI en un Cono Vendido
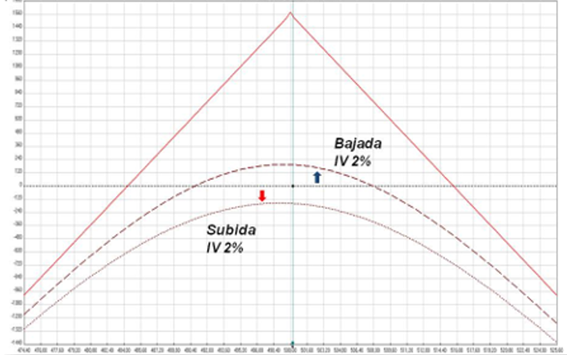
Si la VI baja 2 puntos a un 28%, nos beneficiará. Nuestra posición incrementará en valor ya que vendimos la volatilidad cuando era más cara.
En el trading de opciones es fundamental entender cómo funciona la volatilidad y los efectos que tiene sobre las opciones. En el caso de arriba hemos escogido unas opciones de agosto con tan sólo 15 días hasta su vencimiento. La vega de cada una es 40 (este valor es muy caro). Sin embargo, si escogemos opciones de diciembre o un mes parecido, la vega aumenta mucho, hasta varias veces el tamaño de la del primer mes. Una pequeña variación en la volatilidad afecta muchísimo.
También hay que decir que las variaciones de las volatilidades de opciones en meses con vencimientos más lejanos son más pequeñas que en las de opciones cercanas al vencimiento.
Cada opción tiene su propia VI. Y aunque hay una VI promedio para las opciones de cada valor/subyacente (un promedio de toda la cadena de opciones), es siempre conveniente ver la VI particular de la opción que queremos comprar o vender.
Muchos traders trabajan sólo estrategias de volatilidad. Cuando quieren comprarla con la expectativa de que suba, lo que suelen hacer es comprar opciones de meses muy lejanos para su vencimiento, a veces hasta un año y puede que hasta más. Si piensan que la volatilidad va a bajar, venden las opciones.
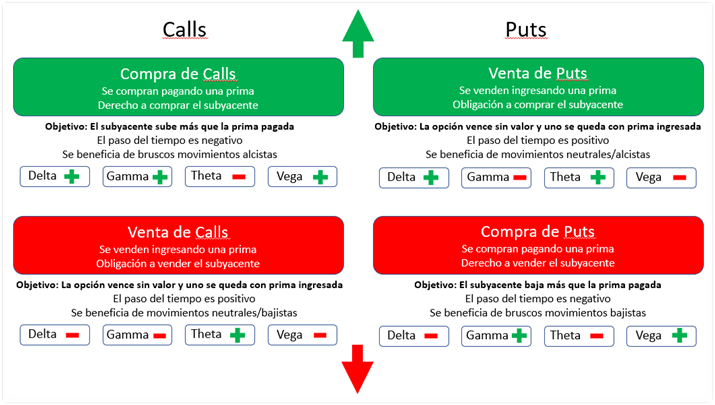
A continuación vemos una tabla que resume las principales características de la compra y venta de calls y puts.
Resumen de la Compra y Venta de Calls y Puts
Ricardo Sáenz de Heredia





